Question

Light of wavelength 652 nm in vacuum is incident on a single slit whose width is 1.60 × 10-5 m. The setup is then immersed in water whose index of refraction is 1.33. What is the angle θ that locates the third dark fringe with respect to the central bright fringe?

Answer 1

To solve this problem it is necessary to apply the concepts related to wavelength, refractive index of the materials and the principle of superposition through interference and the two slit experiment for constructive and destructive interference.

For definition the constructive interference is defined as,

`d sin\theta = m \lambda`

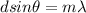
Where,

d = Distance between slits

m = Any integer, which is representing the number of repetition of the spectrum (Number of fringe)

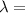`\lambda =` wavelength

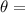`\theta =`Angle

Our values are given as,

`\lamda_l =` 641nm

n = 1.33

m=3

`\lambda_w = (652)/(1.33)`

`\lambda_w = 490.22nm = 429.22*10^(-9)m`

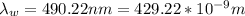
Therefore the angle that locates the third dark fringe with respect to the central bright fringe is

`d sin\theta = m \lambda`

`(1.6*10^(-5))sin\theta = (3) 429.22*10^(-9)`

`\theta = sin^(-1) (((3) 429.22*10^(-9))/((1.6*10^(-5))))`

`\theta = 4.616\°`

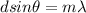
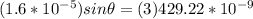
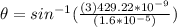
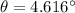
The angle θ that locates the third dark fringe with respect to the central bright fringe is 4.616°