Answer:
Accelerations of both the sides is 0.6125
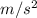 , A moves downwards whereas B moves upwards.
, A moves downwards whereas B moves upwards.
 =6.125 rad/
=6.125 rad/
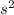
Tension on side A = 4.5 × g= 44.1 m/
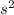
Tension on side B= 2.0 × g= 19.6 m/
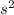
Step-by-step explanation:
As both, the blocks A and B are attached due to the constraint they can only possess a single acceleration a.
Observe the figure attached, let the tension with Block A be
 and the tension attached with Block B be
and the tension attached with Block B be
 .
.
Tensions will be only be due to the weight of the blocks as no other force is present.
 = 4.5 × g= 44.1 m/
= 4.5 × g= 44.1 m/
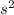
 = 2.0 × g= 19.6 m/
= 2.0 × g= 19.6 m/
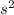
Now, lets make a torque equation about the center of the wheel and find the alpha
 ×R-
×R-
 ×R= MI( Moment of Inertia of Wheel)× Alpha
×R= MI( Moment of Inertia of Wheel)× Alpha
where, R= Radius of the wheel=0.100m and
Alpha(
 )= Angular acceleration of the wheel
)= Angular acceleration of the wheel
MI of the wheel= 0.400 kg/

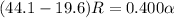

 =6.125 rad/
=6.125 rad/
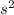
Acceleration = R ×

= 0.1 * 6.125
=0.6125
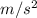
Accelerations of both the sides is 0.6125
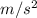 , A moves downwards whereas B moves upwards.
, A moves downwards whereas B moves upwards.