Question

Find the lateral area and the surface area of the regular hexagonal pyramid.

Question 8 options:

lateral area = 385.1 cm2; surface area = 805 cm2

lateral area = 231.6 cm2; surface area = 441 cm2

lateral area = 210 cm2; surface area = 325.5 cm2

lateral area = 21.8 cm2; surface area = 231.2 cm2

Answer 1

lateral area = 210 cm2; surface area = 325.5 cm2 is correct.

Explanation:

Answer 2

Part 1) The lateral area is
`LA=210\ cm^2`

Part 2) The surface area is
`SA=325.5\ cm^2`

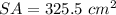
so

lateral area = 210 cm2; surface area = 325.5 cm2

Explanation:

Part 1) Find the lateral area of the regular hexagonal pyramid

The lateral area is equal to the area of its six triangular faces

so

`LA=6[(1)/(2)bh]`

we have

`b=7\ cm\\h=10\ cm`

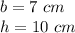
substitute

`LA=6[(1)/(2)(7)(10)]`

`LA=210\ cm^2`

Part 2) Find the surface area of the regular hexagonal pyramid

The surface area is equal to the lateral area plus the area of the hexagonal base

so

`SA=LA+B`

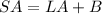
where

B is the area of the hexagonal base

Find the area of the hexagonal base

The area of the regular hexagon is equal to the area of six equilateral triangles

`B=6[(1)/(2)(b)(h)]`

we have

`b=7\ cm\\h=5.5\ cm`

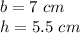
substitute

`B=6[(1)/(2)(7)(5.5)]`

`B=115.5\ cm^2`

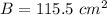
The surface area is equal to

`SA=210+115.5=325.5\ cm^2`