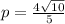Question

I HAVE MY MOCKS TOMORROW AND I WILL DO THE SAME TEST THAT I HAVE KNOW HEEEEELP

Answer 1

`p=(4√(10))/(5)`

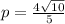
Explanation:

step 1

Find the radius of the circle

Remember that AB is a tangent to the circle at point B

so

AB is perpendicular to OA

The radius of the circle is equal to the segment OA

In the right triangle OAB

`sin(30\°)=(OA)/(OB)`

`OA=(OB)sin(30\°)`

substitute the values

`OA=(16)0.5=8\ units`

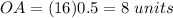
step 2

Find the value of p

In the right triangle OPQ

see the attached figure to better understand the problem

Applying the Pythagoras Theorem

`OP^2=OQ^2+PQ^2`

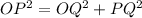
substitute the values

Remember that OP is the radius

`8^2=p^2+(3p)^2`

`64=p^2+9p^2`

`64=10p^2`

`p^2=(64)/(10)`

`p=(8)/(√(10))`

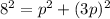
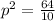
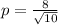
simplify

`p=(4√(10))/(5)`