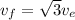If gravitational effects from other objects are negligible, the speed of the rock at a very great distance from the planet will approach a value of
Step-by-step explanation:
To express velocity which is too far from the planet and escape velocity by using the energy conservation, we get
Rock’s initial velocity ,
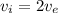 . Here the radius is R, so find the escape velocity as follows,
. Here the radius is R, so find the escape velocity as follows,
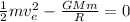

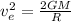

Where, M = Planet’s mass and G = constant.
From given conditions,
Surface potential energy can be expressed as,
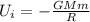
R tend to infinity when far away from the planet, so
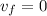
Then, kinetic energy at initial would be,
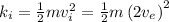
Similarly, kinetic energy at final would be,
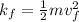
Here,
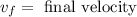
Now, adding potential and kinetic energies of initial and final and equating as below, find the final velocity as

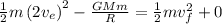

'm' and
 as common on both sides, so gets cancelled, we get as
as common on both sides, so gets cancelled, we get as
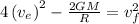
We know,
 , it can be wriiten as
, it can be wriiten as
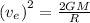 , we get
, we get
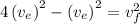
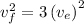
Taking squares out, we get,