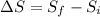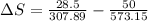Question

A reversible power cycle whose thermal efficiency is 43% receives 50 kJ by heat transfer from a hot reservoir at 300oC and rejects energy by heat transfer to a cold reservoir at temperature TC. Determine the energy rejected, in kJ, and TC, in oC. Determine the entropy production for the cycle, σcycle, in kJ/K.

Answer 1

To solve this problem it is necessary to take into account the Efficiency values in the energy cycles.

Efficiency can be defined as,

`\eta = 1 - (Q_c)/(Q_h) = 1- (T_c)/(T_h)`

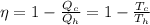
Where,

Q = Heat Exchange

T = Temperature

The efficiency for this system is 0.43 then,

`0.43 = 1-(Q_c)/(50)`

Re-arrange to find
`Q_c`

`Q_c = 50*(1-0.43)`

`Q_c = 28.5kJ`

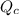
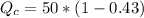
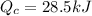
And the temperature would be given as,

`\eta = 1- (T_c)/(T_h)`

`0.43 = 1 - (T_c)/(573.15K)`

`T_c = 513.15K(1-0.43)`

`T_c = 307.89K`

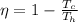
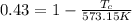
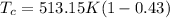
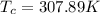
The entropy would be given as

`\Delta S = S_f - S_i`

`\Delta S = (Q_c)/(T_c)-(Q_h)/(T_h)`

`\Delta S = (28.5)/( 307.89)-(50)/(573.15)`

`\Delta S = 5.32*10^(-3) kJ/K`