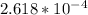To solve this problem it is necessary to apply the concepts related to the wave function of a particle and the probability of finding the particle in the ground state.
The wave function is given as
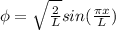
Therefore the probability of finding the particle must be
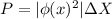

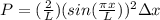
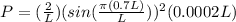
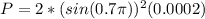
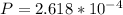
Therefore the probability is