Question

A clinical trial tests a method designed to increase the probability of conceiving a girl. In the study 300 babies were​ born, and 270 of them were girls. Use the sample data to construct a 99​% confidence interval estimate of the percentage of girls born. Based on the​ result, does the method appear to be​ effective?

Answer 1

99% confidence interval would be given (0.98;1).

We are confident that about 98% to 100% of the babies born using this new method will be girls. So is very effective since increase the probability of getting a girl by almost the double.

Explanation:

1) Data given and notation

n=300 represent the random sample taken

X=270 represent the number of girls born in the sample selected

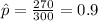`\hat p=(270)/(300)=0.9` estimated proportion of girls born with the new method

Confidence =99% or 0.99

p= population proportion of girls born with the new method proposed

2) Confidence interval

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

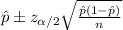
For the 99% confidence interval the value of
`\alpha=1-0.99=0.01` and
`\alpha/2=0.005`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=2.58`

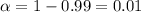And replacing into the confidence interval formula we got:

`0.99 - 2.58 \sqrt{(0.99(1-0.99))/(300)}=0.98`

`0.99 + 2.58 \sqrt{(0.99(1-0.99))/(300)}=1.00`

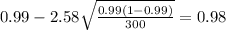
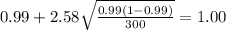
And the 99% confidence interval would be given (0.98;1.00).

We are confident that about 98% to 100% of the babies born using this new method will be girls. So is very effective since increase the probability of getting a girl by almost the double.