Question

Find two positive integers that satisfy the requirement.

The product of two consecutive odd integers is 483.

Answer 1

The two positive integers that satisfy the requirement are 21 and 23

Explanation:

Let

x ----> the first consecutive odd integer

x+2 ---> the second consecutive odd integer

we know that

`x(x+2)=483`

Apply distributive property left side

`x^2+2x=483`

`x^2+2x-483=0`

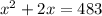
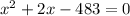
we know that

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`x^2+2x-483=0`

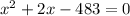
so

`a=1\\b=2\\c=-483`

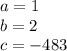
substitute in the formula

`x=\frac{-2(+/-)\sqrt{2^(2)-4(1)(-483)}} {2(1)}`

`x=\frac{-2(+/-)√(1,936)} {2)}`

`x=\frac{-2(+/-)44} {2)}`

`x=\frac{-2(+)44} {2)}=21`

`x=\frac{-2(-)44} {2)}=-23`

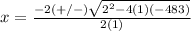
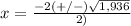
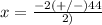
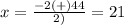
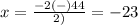
so

x=21

x+2=23

therefore

The two positive integers that satisfy the requirement are 21 and 23