Answer: No, these response does not provide strong evidence that the 34% figure is not accurate for this region.
Explanation:
Since we have given that
p = 0.34
x= 228
n = 750
So,
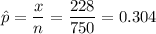
So, hypothesis would be
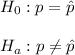
So, test statistic value would be
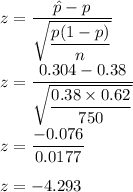
At 95% confidence , z = 1.96
So, 1.96>-4.293.
So, we accept the null hypothesis.
No, these response does not provide strong evidence that the 34% figure is not accurate for this region.