Question

Pleaseeeeee help.... I already know part A answer just don't know part B.

a) Jennifer has a taco stand. she has found that her daily costs can be modeled by c(x)=x^2-40x+610, where c(x) is the cost, in dollars, to sell x units of taco. if she wants to keep her daily costs at $300, how many units of tacos does she need to sell?


b) What answer to part a makes the most sense from Jennifer's point of view?

Answer 1

a) 29.486 and 10.513. Rounded to 29 and 11

b) 29 Tacos make more sense.

Explanation:

a) The value x of units must satisfy this equation:

c(x) = 300

therefore,

`300 = x^2-40x+610`

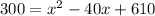
or, equivalently,

`x^2-40x+310 = 0`

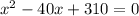
the roots of this quardratic function are

`r_1, r_2 = (40^+_- √((-40)^2-4*1*310))/(2*1) = (40^+_- √(360))/(2) = 20^+_- √(90) \simeq 20^+_- 9.48632`

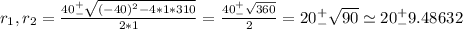
Thus, r1 = 29.486, and r2 = 10.513. Assuming the results have to be integers, Jennifer should sell 29 units or 11 to keep her daily costs below $300 the nearest possible. Note that c(29) = c(11) = 291.

b) I will assume that Jennifer wins money proportionally to the amount she sell (without discounting from costs). If this is true, then it would make more sense to sell 29 units because that would give her more gain, including costs.

Also, since the function is quadratic, then it will decrease until certain point, which means that selling more will make her daily costs decrease! For example c(20) = 210. That doesnt make a lot of sense. This model of costs might make more sense for higher values of x, so in any case she should pick the biggest value.