Question

A track is traveling a. a speed of 25.0 m/s along a level road. A crate is resting on the bed of the truck, and the coefficient of static friction between the crat. And the truck bed is 0.650. Determine the shortest distance in which the truck can come to a halt without causing the crate to slip forward relative to the truck.

Answer 1

To solve this problem it is necessary to apply the concepts related to

conservation of energy, for this case manifested through work and kinetic energy.

`W = \Delta KE`

`W = F*d`

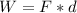
Where,

F= Force (Frictional at this case
`F_r = \mu N`)

d= Distance

`\Delta KE = (1)/(2) mv^2`

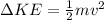
Where,

m = mass

v = velocity

Equation both terms,

`F*d = (1)/(2)mv^2`

`\mu mg *d = (1)/(2)mv^2`

`\mu g * d = (1)/(2)v^2`

`d = (1)/(2) (v^2)/(\mu g)`

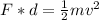
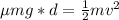
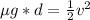
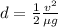
Replacing with our values we have that

`d = (1)/(2) (25^2)/(0.65*9.8)`

`d = 49.05m`

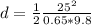
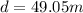
Therefore the shortest distance in which the truck can come to a halt without causing the crate to slip forward relative to the truck is 49.05m