Answer:
1) Real and same.
2) Real and distinct
3) Real and distinct
4) Real and distinct
5) Real and distinct
6) Real and distinct
7) Real and distinct
8) Real and distinct
Explanation:
If a quadratic equation is in the form of ax² + bx + c = 0, then Discriminant of the equation D = b² - 4ac, which governs the nature of roots the equation has.
If D > 0, then there will be two different real roots.
If D = 0, then two same and real roots.
If D < 0, then two distinct but imaginary roots.
Now, 1) x² + 6x + 9 = 0 has D = 6² - 4 × 9 × 1 = 0. So, there will be two same and real roots.
2) 5x² - x = 4x² + 2
⇒ x² - x - 2 = 0
It has D = (-1)² - 4 × 1 × (-2) = 9. Therefore, the roots will be two distinct and real.
3)
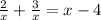
⇒ 5 = x² - 4x
⇒ x² - 4x - 5 = 0.
So, D = (-4)² - 4 × (1) × (- 5) = 36. So, the equation has two real and distinct rools.
4) x(x - 5) = 4(5 - x)
⇒ x² - x - 20 = 0
Hence, D = (-1)² - 4 × 1 × (-20) = 81
So, the roots will be real and distinct.
5) x² + 7x + 1 = 0 has D = 7² - 4 × 1 × 1 = 45
So, the roots will be real and distinct.
6) 2x² + 9x + 3 = 0, has D = 9² - 4 × 2 × 3 = 57.
Hence, the roots will be real and distinct.
7) 5x² - 6 = 13x
⇒ 5x² - 13x - 6 = 0
So, D = (-13)² - 4 × 5 × (-6) = 289
So, the roots will be real and distinct.
8) x² - x = 3(x + 7)
⇒ x² - 4x - 21 = 0
It has D = (-4)² - 4 × 1 × (-21) = 100
So, the roots will be real and distinct. (Answer)