Question

An astronaut drops a hammer on the moon . It takes 1 second to hit the ground after being dropped, and it is going 1.6m/s when it lands. What is the acceleration due to gravity on thr moon?

Answer 1

the value of acceleration due to gravity in moon is 1.6m/
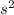`s^(2)` along downward direction

Step-by-step explanation:

Here, the acceleration is constant and it is equal to acceleration due to gravity in moon. Therefore the question depicts a situation of uniformly accelerated motion in a straight line. So, let us refresh the three equations of uniformly accelerated straight line motion.

v = u + at

`s = ut + (1)/(2)at^(2)`

`v^(2) = u^(2) +2as`

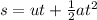
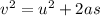
where,

u = initial velocity

v = final velocity

s = displacement

a = acceleration

t = time

Since we are dealing with vectors (velocity, acceleration and displacement), we have to take their directions in to account. So we must adopt a coordinate system according to our convenience. Here, we are taking point of throwing as origin, vertically upward direction as positive y axis and vertically downward direction as negative y axis.

t = 1s

u = 0 (since the hammer is dropped)

v = -1.6m/s (since its direction is downward)

a = ?

The only equation that connects all the above quantities is

v = u + at

therefore,

a =
`(v - u)/(t)`

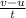
substituting the values

a =
`(-1.6 - 0)/(1)`

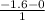
a = -1.6m/
`s^(2)`

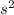
Thus, the value of acceleration due to gravity in moon is 1.6m/
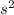`s^(2)`. The negative sign indicates that it is along downward direction.