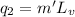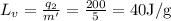Question

Consider a 10 gram sample of a liquid with specific heat 2 J/gK. By the addition of 400 J, the liquid increases its temperature by 10 K and then boils. Half of the liquid boils away before all the heat is used up. What is the heat of vaporization of the liquid?A.10 J/gB.20 J/gC.80 J/gD.200 J/gE.40 J/g© 2018.Grand Canyon University. All Rights Reserved.

Answer 1

40 J/g is the heat of vaporization of the liquid.

Answer: Option D

Step-by-step explanation:

Given that mass of liquid sample: m = 10 g

And, Specific heat of the liquid: S = 2 J/g K

Also, the increase in the temperature of the liquid,
`\Delta T = T_(2)-T_(1) = 10 K`

Therefore, the total amount of heat energy required is given by:

`q_(1) = m * S *\left(T_(2)-T_(1)\right) = 10 * 2 * 10 = 200 J`

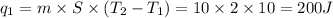
According to the given data in the question,

Total heat energy supplied, q = 400 J

Rest of heat would be
`q_(2)=q-q_(1)=400-200=200 \mathrm{J}`

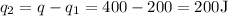
Now, 200 J vaporizes the mass, half of the liquid from full portion boiled away. So,

`m^(\prime) = (10)/(2) = 5 \mathrm{g}`

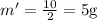
Latent heat of vaporization of the liquid is
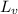`L_(v)`. It can be calculated as below,

`q_(2) = m^(\prime) L_(v)`

`L_(v) = (q_(2))/(m^(\prime)) = (200)/(5) = 40 \mathrm{J} / \mathrm{g}`