Answer:
The Time period required for decay of Iodine-125 to half of its value is 60 days .
Explanation:
Given as :
The initial quantity of iodine-125 = 0.4 gram
The rate of decay = 1.15 %
Let The time period for decay = x day
The finial quantity after decay = half of initial quantity
I.e The finial quantity after decay = 0.2 gram
Now ,
The final quantity after decay = initial quantity ×

Or, 0.2 gm = 0.4 gm ×

or,
 =
=

Or, 0.5 =

Or,
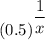 = 0.9885
= 0.9885
Taking log both side
log (
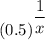 ) = Log 0.9885
) = Log 0.9885
or,
 × log 0.5 = - 0.0050233
× log 0.5 = - 0.0050233
or,
 × ( - 0.301029 ) = - 0.0050233
× ( - 0.301029 ) = - 0.0050233
or, x =
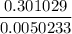
∴ x = 59.92 ≈ 60 days
Hence The Time period required for decay of Iodine-125 to half of its value is 60 days . Answer