Question

The heights of a random sample of 50 college students showed a mean of 167.4 centimeters and a standard deviation of 6.9 centimeters. ​(a) Construct a 98​% confidence interval for the mean height of all college students. ​(b) What can we assert with 98​% confidence about the possible size of our error if we estimate the mean height of all college students to be 167.4 ​centimeters?

Answer 1

Answer: a) (165.13, 169.67), b) Error = 2.274.

Explanation:

Since we have given that

Mean = 167.4 cm

Standard deviation = 6.9 cm

N = 50

we need to construct 98% confidence interval.

So, Interval would be

`\bar{x}\pm2.33(\sigma)/(√(n))\\\\=167.4\pm 2.33* (6.9)/(√(50))\\\\=167.4\pm 2.274\\\\=(167.4-2.274,167.4+2.274)\\\\=(165.13,169.67)`

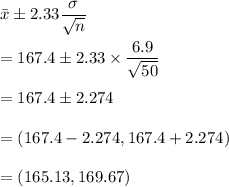
b) Margin of error would be

`z* (\sigma)/(√(n))\\\\=2.33* (6.9)/(√(50))\\\\=2.274`

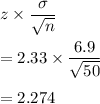
Hence, a) (165.13, 169.67), b) Error = 2.274.