Answer:
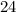
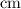
Explanation:
Given: The distance from the centroid of a triangle to its vertices are
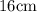 ,
,
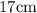 , and
, and
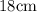 .
.
To Find: Length of shortest median.
Solution:
Consider the figure attached
A centroid is an intersection point of medians of a triangle.
Also,
A centroid divides a median in a ratio of 2:1.
Let G be the centroid, and vertices are A,B and C.
length of
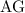
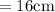
length of
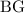

length of
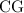
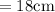
as centrod divides median in ratio of

length of
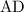
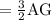

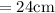
length of
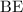

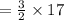
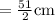
length of
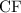
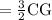
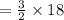
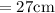
Hence the shortest median is
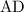 of length
of length
