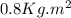Question

The triceps muscle in the back of the upper arm extends the forearm. This muscle in a professional boxer exerts a force of 2.00 ✕ 103 N with an effective perpendicular lever arm of 5.00 cm, producing an angular acceleration of the forearm of 125 rad/s2. What is the moment of inertia (in kg·m2) of the boxer's forearm?

Answer 1

To solve the problem it is necessary to apply all the concepts related to the definition of Torque, both linear and angular.

From the linear definition the torque is defined as

`\tau = F*r`

Where,

F = Force

r = radius

On the other hand we have that,

`\tau = I \alpha`

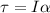
Where,

I = Moment of inertia

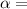`\alpha =` Angular Acceleration

Using the first equation we can find the Torque, there,

`\tau = F*r`

`\tau = (2*10^3)(0.05)`

`\tau = 100Nm`

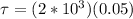
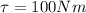
Therefore the Inertia moment can be calculated from the second equation,

`\tau = I \alpha`

`I = (\tau)/(\alpha)`

`I = (100)/(125)`

`I = 0.8 kg.m^2`

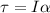
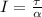
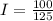
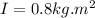
Therefore the value of moment of inertia is
`0.8 Kg.m^2`