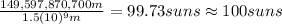Answer: 100 suns
Step-by-step explanation:
We can solve this with the following relation:
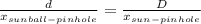
Where:
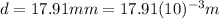 is the diameter of a dime
is the diameter of a dime
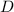 is the diameter of the Sun
is the diameter of the Sun
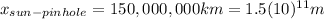 is the distance between the Sun and the pinhole
is the distance between the Sun and the pinhole
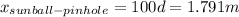 is the amount of dimes that fit in a distance between the sunball and the pinhole
is the amount of dimes that fit in a distance between the sunball and the pinhole
Finding
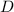 :
:
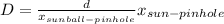
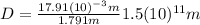
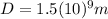 This is roughly the diameter of the Sun
This is roughly the diameter of the Sun
Now, the distance between the Earth and the Sun is one astronomical unit (1 AU), which is equal to:
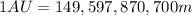
So, we have to divide this distance between
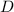 in order to find how many suns could it fit in this distance:
in order to find how many suns could it fit in this distance: