Question

A block of mass 11.8 kg slides from rest down a frictionless 35.6∘ incline and is stopped by a strong spring with ????=3.11×104 N/m. The block slides 3.05 m from the point of release to the point where it comes to rest against the spring. When the block comes to rest, how far has the spring been compressed?

Answer 1

To solve this problem it is necessary to apply the concepts related to Work, Kinetic energy in springs and the conservation of Energy.

By definition work in a body is defined by

`W = F*d`

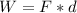
Where,

F = Force

d = Distance

On the other hand we have that

`E = (1)/(2)kx^2`

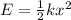
Where,

k = Spring constant

x = Displacement

Since it is an inclined plane, we can intuit that the component of the distance that allows the calculation of the work is the opposite of the angle (vertical), so

`W = Fdsin\theta`

`W = mg d sin\theta`

`W = (11.8)(9.8)(3.05)sin35.6`

`W = 205.31J`

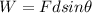
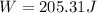
From the second equation we can calculate the displacement, then

`E = (1)/(2)kx^2`

`205.31 = (1)/(2) 3.11*10^4 (x)^2`

`x = \sqrt{(2*205.31)/(3.11*10^4)}`

`x = 0.1149m = 11.49cm`

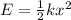
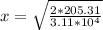
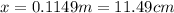
Therefore the block come to rest when the spring has been compressed around to 11.49cm