Final answer:
The confidence interval for percentage of U.S. adults who were victims of crime at the 90% confidence level is (0.114, 0.15). The lower bound of the confidence interval is 0.114.
Step-by-step explanation:
To estimate the percentage of U.S. adults who were victims of crime at the 90% confidence level, we can use the formula for a confidence interval:

where CI is the confidence interval, p is the sample proportion, Z is the Z-score corresponding to the desired confidence level, and n is the sample size. In this case, p = 0.132, Z = 1.645 (corresponding to a 90% confidence level), and n = 1105. Plugging in these values, we can calculate the confidence interval as:
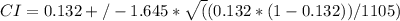
Simplifying the expression gives us:
CI = 0.132 ± 0.018
Therefore, the confidence interval for the percentage of U.S. adults who were victims of crime at the 90% confidence level is (0.114, 0.15). The lower bound of the confidence interval is 0.114.