Question

Explain the properties and the processes you have to use to solve the following logarithmic equation: log base 3 of x + log base 3 of 4 - 2log base 3 of 3 = 2

Answer 1

x = 20.25

Explanation:

Given logarithmic equation is

`\log_(3) x + \log_(3) 4 - 2 \log_(3) 3 = 2`

⇒
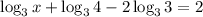
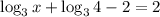`\log_(3) x + \log_(3) 4 - 2  = 2`{Since we know the logarithmic property
`\log_(a) a = 1`}

⇒
`\log_(3) x + \log_(3) 4 = 4`

⇒
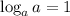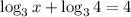
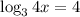`\log_(3) 4x = 4` {Since, we know the logarithmic property that
`\log_(a) x +\log_(a) y = \log_(a) (xy)`}

⇒
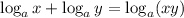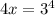`4x = 3^(4)` {Converting from logarithm to exponent form}

{Since we know that, if
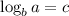`\log_(b) a = c` then we can write
`a = b^(c)`}

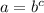⇒ 4x = 81

⇒ x = 20.25 (Answer)