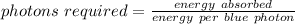Question

A glass plate has a mass of 0.50 kg and a specific heat capacity of 840 J/(kg·C°). The wavelength of infrared light is 18 × 10-5 m, while the wavelength of blue light is 4.6 × 10-7 m. Find the number of infrared photons and the number of blue photons needed to raise the temperature of the glass plate by 2.0 °C, assuming that all the photons are absorbed by the glass.

Answer 1

So,

We are given:

mass of plate = 0.50 kg

specific heat capacity = 840 J/(kg °C)

wavelength of infrared = 18 * 10^-5 m

wavelength of blue light = 4.6 * 10^-7 m

ΔT = +2.0 °C

Additionally, we should already know:

q = mcΔT, where q is the energy absorbed (+) or released (-) by the system, m is the mass of the system, c is the specific heat capacity, and deltaT is the change in temperature.

E = hv, where E is the energy in J, h is Planck's constant, and v is the frequency of the light

c = wv, where c is the speed of light, w is the wavelength, and v is the frequency

We need to find the number of infrared photons and the number of blue photons required to result in the given temperature change.

Key idea: if we can find the energy if each photon, we can find the number of photons required to raise the temperature of the plate.

I will start with the infrared photons. We can do this with the assumed equations. We want to find E. We have w, and we should have h and c.

First, let's find v.

`c = w_(infrared)v_(infrared)`

`v=(c)/(w)`

`v_(infrared)=(3.00*10^8 (m)/(s))/(18*10^(-5) m)=1.67*10^(12) s^(-1)`

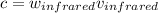
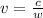
Next, let's find E.

`E_(infrared)=hv_(infrared)`

`E=(6.626*10^(-34) J*s)(1.67*10^(12) s^(-1))=1.10*10^(-21)\ J`

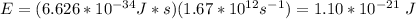
Now, let's find the amount of energy absorbed by the plate.

`q=mc\Delta T`

`q=0.50 kg * 840 (J)/(kg\ ^o C)*2.0\ ^o C = 840\ J`

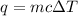
Now, we can find the number of infrared photons required.

`photons\ required = (energy\ absorbed)/(energy\ per\ infrared\ photon)`

`photons=(840\ J)/(1.10*10^(-21) (J)/(infrared\ photon))=7.61*10^(23) \ infrared\ photons`

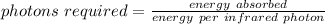
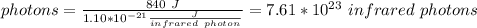
So the number of infrared photons required is 7.57 * 10^23 photons.

We can do a similar procedure for the blue light.

Find v.

`c = w_(blue)v_(blue)`

`v=(c)/(w)`

`v_(infrared)=(3.00*10^8 (m)/(s))/(4.6*10^(-7) m)=6.52*10^(14) s^(-1)`

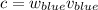
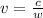
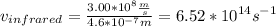
Find E.

`E_(blue)=hv_(blue)`

`E=(6.626*10^(-34)\ J*s)(6.52*10^(14)\ s^(-1))=4.32*10^(-19)\ J`

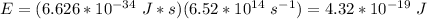
The energy absorbed by the plate is the same 840 J.

Now, find the number of blue photons required.

`photons\ required = (energy\ absorbed)/(energy\ per\ blue\ photon)`

`photons=(840\ J)/(4.32*10^(-19)\ (J)/(blue\ photon))=1.94*10^(21) \ blue\ photons`