Answer:
a) Flow rate of aorta = 9.818 x
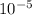
 /s
/s
b) Flow rate of capillariy = 2.827 x
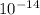
 /s
/s
c) Number of capillaries = 3.473 x

Step-by-step explanation:
This question focuses on the flow rate of a fluid. So let us look what flow rate is.
Flow rate is the volume of fluid that flows through the tube per unit time.
i.e. Flow rate =
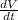
where,
V = Volume of the fluid
t = time
We know that Volume = Area x distance
therefore,
Flow rate =
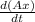
where,
A = cross sectional area of the tube
x = distance
Since in this problem area is a constant, we can take A out of differentiation.i.e.
Flow rate =

Now, we got
 which is equal to velocity of the fluid.
which is equal to velocity of the fluid.
Thus,
Flow rate =
 = Av
= Av
where, v = velocity
a) diameter of aorta = 2.50cm = 2.5x

Area, A = π
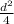 = π
= π
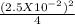
= 4.909 x
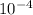

v = 20.0 cm/s = 0.2m/s
We know that Flow rate = Av = 4.909 x
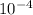 x 0.2 = 9.818 x
x 0.2 = 9.818 x
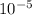
 /s
/s
b) diameter of capillary = 6.00 × 10−6 m
Area, A = π
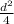 = π
= π
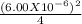 = 2.827x
= 2.827x


v = 1.00 mm/s =
 m/s
m/s
We know that Flow rate = Av = 2.827x
 x
x
 = 2.827 x
= 2.827 x
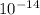
 /s
/s
c)Since the fluid is incompressible, the flow rate before and after should be same. Let there be n capillaries.
Then total flow rate in the capillaries = n x 2.827 x
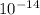
 /s
/s
Flow rate in aorta = 9.818 x
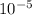
 /s
/s
These two should be equal. i.e.
n x 2.827 x
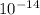 = 9.818 x
= 9.818 x
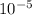
n =
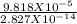
n = 3.473 x
