Candy draws a square design with a side length of x inches for the window at the pet shop. She takes the design to the printer and asks for a sign that has an area of 16x2 – 40x + 25 square inches. What is the side length, in inches, of the pet shop sign?
Answer:
the length of the sign is
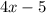 inches
inches
Explanation:
Given
Area of the square of design =

First we find the roots of equation

The roots of the quadratic equation
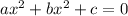 are given by
are given by
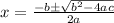
where

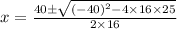
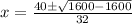


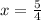
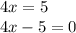
That is, the factors of the polynomial
 are
are
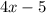 and
and
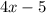 .
.
So, Area of the square design =
 =
=

Area of a square = Length^2
Thus, the length of the sign is
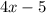 inches
inches