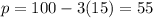Question

Determinar el precio del artículo y la cantidad que debe producirse para obtener la máxima utilidad.?

la demanda de un mercado monopolizado sigue la ley:
p = 100-3x, y el monopolista produce x unidades a un costo total de:
C= 1/2x² -3x + 1500 Determinar el precio del artículo y la cantidad que debe producirse para obtener la máxima utilidad.

Answer 1

Se deben producir 15 artículos a un precio de 55 cada uno

Explanation:

Parece que hay un error en el planteamiento del problema porque se obtienen ganancias negativas en cualquier solución óptima. Sin embargo, te mostraré el procedimiento correcto necesario.

La ecuación de la demanda es

`p = 100-3x`

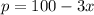
El ingreso es el producto del precio por el número de artículos producidos

`I(x)=px=100x-3x^2`

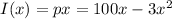
El costo de producir x unidades viene dado por

`C= (1)/(2)x^2 -3x + 1500`

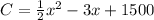
La Ganancia es la diferencia entre el ingreso y los costos

`G(x)=I-C=100x-3x^2-\left ( (1)/(2)x^2 -3x + 1500 \right )`

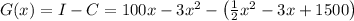
Operando

`G(x)=-(7)/(2)x^2+103x- 1500`

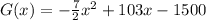
Para optimizar la ganancia, se obtiene su primera derivada y se iguala a cero

`G'(x)=-7x+103`

`-7x+103=0`

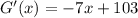
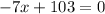
Obtenemos así el valor óptimo de producción

`x=(103)/(7)=14.7`

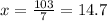
Siendo x un número entero por ser el número de unidades, probamos con los enteros que rodean a la respuesta obtenida

`G(14)=-744`

`G(15)=-742.5`

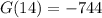
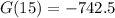
La menos negativa ganancia sería el valor óptimo, que según mencionamos, es negativa. Luego el valor óptimo es x=15

El precio con x=15 es

`p = 100-3(15)=55`