Question

The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.0 inches and a standard deviation of 0.9 inches. A sample of 36 metal sheets is randomly selected from a batch. What is the probability that the average length of a sheet is between 29.82 and 30.27 inches long?

Answer 1

Answer: 0.8490

Explanation:

Given : The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.0 inches and a standard deviation of 0.9 inches.

i.e.
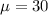`\mu=30` and
`\sigma=0.9`

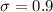
Let x denotes the lengths of aluminum-coated steel sheets.

Required Formula :
`z=(x-\mu)/((\sigma)/(√(n)))`

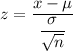
For n= 36 , the probability that the average length of a sheet is between 29.82 and 30.27 inches long will be :-

`P(29.82<x<30.27)=P((29.82-30)/((0.9)/(√(36)))<(x-\mu)/((\sigma)/(√(n)))<(30.27-30)/((0.9)/(√(36))))\\\\=P(-1.2<z<1.8)\\\\=P(z<1.8)-P(z<-1.2)\\\\=P(z<1.8)-(1-P(z<1.2))\ \ {[\because\ P(Z<-z)=1-P(Z<z)]}\\\\= 0.9641-(1-0.8849)[\text{By using z-table.}]\\\\=0.8490`

∴ Required probability = 0.8490