Question

A jet pilot takes his aircraft into a vertical loop. If the jet is moving at a speed of 700km/hr at the lowest point in the loop, determine the radius of the circle so that the acceleration which the pilot experiences at the lowest point of the loop does not exceed 6 time the acceleration due to gravity or (6g’s).

Answer 1

The radius of circle is 643 m.

Step-by-step explanation:

The centripetal acceleration of the jet is

`a=(V^(2))/(r)`

Where,

a is "centripetal acceleration"

V is "speed "

r is "radius of the circle "

Given values ,

Speed of the jet (v) = 700 km/h

(1 km = 1000 m; 1 h = 3600 sec. To convert km/h into m/sec, multiply the number by 5 and then divide it by 18.)

Speed of the jet (v)
`=\left(700 * (5)/(18)\right) \mathrm{m} / \mathrm{s}`

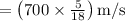
V = 194.444 m/s

a = 6g's

`\text { (g is referred to as the acceleration of gravity. Its value is }\left.9.8 \mathrm{m} / \mathrm{s}^(2) \text { on Earth }\right)`

`a=6 * 9.8 \mathrm{m} / \mathrm{s}^(2)`

`a=58.8 \mathrm{m} / \mathrm{s}^(2)`

`\text { The radius of circle is a }=(V^(2))/(r)`

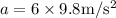
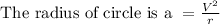
Substitute the given values in the formula,

`a=(194.444^(2))/(58.8)`

`a=(37808.46)/(58.8)`

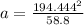
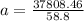
a = 643 m

The radius of circle is 643 m.