Question

Jim's soccer team is making fruit baskets for a fundraiser. They have 88 peaches, 60 bananas, and 54 kiwis to use. If each baskets have the same numbers of each type, what is the greatest number of fruit baskets they can make?

Answer 1

The greatest number of fruit baskets they can make is 2 with each one having 44 peaches, 30 bananas and 27 kiwis

Solution:

Jim’s fruit basket has 88 peaches, 60 bananas and 54 Kiwis to use.

If each basket have same number of each type, we have to determine the greatest number of fruit baskets they can make

We need to find greatest common factor of 88, 60 and 54

When we find all the factors of two or more numbers, and some factors are the same ("common"), then the largest of those common factors is the Greatest Common Factor.

Greatest common factor of 88, 60 and 54:

The factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54

The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

The factors of 88 are: 1, 2, 4, 8, 11, 22, 44, 88

Then the greatest common factor is 2

On dividing the number of fruits by 2 we get

`\begin{array}{l}{\text { Apples in each basket }=(88)/(2)=44} \\\\ {\text { Bananas in each basket }=(60)/(2)=30} \\\\ {\text { Kiwis in each basket }=(54)/(2)=27}\end{array}`

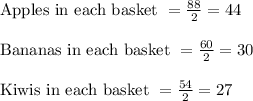
Hence, there can be 2 basket with each one having 44 peaches, 30 bananas and 27 kiwis