Question

Under ideal conditions (no atmospheric interference of any kind), if I hit a golf ball at an angle of 25 degrees at an initial speed of 23 m/s, it will travel the same distance as a golf ball struck so it has an initial speed of 23 m/s at an angle of ___ degrees.

Answer 1

- 25° from positive X axis .

Step-by-step explanation:

If a projectile projects with velocity u and at angle of projection Ф, it strikes the ground with the same velocity and at same angle but in downward direction.

So, it makes an angle of - 25°.

Answer 2

The required angle is (90-25)° = 65°

Step-by-step explanation:

The given motion is an example of projectile motion.

Let 'v' be the initial velocity and '∅' be the angle of projection.

Let 't' be the time taken for complete motion.

Let 'g' be the acceleration due to gravity

Taking components of velocity in horizontal(x) and vertical(y) direction.

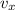`v_(x)` = v cos(∅)

`v_(y)` = v sin(∅)

We know that for a projectile motion,

t =
`(2vsin(∅))/(g)`

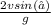
Since there is no force acting on the golf ball in horizonal direction.

Total distance(d) covered in horizontal direction is -

d =
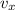`v_(x)`×t = vcos(∅)×
`(2vsin(∅))/(g)` =
`(v^(2)sin(2∅) )/(g)`.

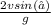If the golf ball has to travel the same distance 'd' for same initital velocity v = 23m/s , then the above equation should have 2 solutions of initial angle 'α' and 'β' such that -

α +β = 90° as-

d =
`(v^(2)sin(2α) )/(g)` =
`(v^(2)sin(2[90-β]) )/(g)` =
`(v^(2)sin(180-2β) )/(g)` =
`(v^(2)sin(2β) )/(g)` .

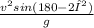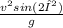∴ For the initial angles 'α' or 'β' , total horizontal distance 'd' travelled remains the same.

∴ If α = 25° , then

β = 90-25 = 65°

∴ The required angle is 65°.