Question

Train cars are coupled together by being bumped into one another. Suppose two loaded train cars are moving toward one another, the first having a mass of 135,000kg and a velocity of 0.305m/s, and the second having a mass of 100,000kg and a velocity of −0.210m/s. (The minus indicates direction of motion.) What is their final velocity?

Answer 1

0.0859 m/s

Step-by-step explanation:

mass of first train, m1 = 135000 kg

mass of second train, m2 = 100000 kg

initial velocity of first train, u1 = 0.305 m/s

initial velocity of second train, u2 = - 0.210 m/s

Let the final velocity after coupling is v.

Use the conservation of momentum

m1 x u1 + m2 x u2 = (m1 + m2) x v

135000 x 0.305 - 100000 x 0.210 = (135000 + 100000) x v

41175 - 21000 = 235000 v

v = 0.0859 m/s

Thus, the velocity after coupling is 0.0859 m/s.

Answer 2

final velocity = 0.08585m/s

Step-by-step explanation:

We are taking train cars as our system. In this system no external force is acting. So we can apply the law of conservation of linear momentum.

The law of conservation of linear momentum states that the total linear momentum of a system remains constant if there is no external force acting on the system. That is total linear momentum before = total linear momentum after

total linear momentum before = linear momentum of first train car + linear momentum of second train car

We know that linear momentum = mv

where,

m = mass

v = velocity

thus,

total linear momentum before = m₁v₁ + m₂v₂

m₁ = mass of first train car = 135,000kg

v₁ = velocity of first train car = 0.305m/s

m₂ = mass of first second car = 100,000kg

v₂ = velocity of second train car = −0.210m/s

Note: Momentum is a vector. So while adding momentum we should take account of its direction too. Here since second train car is moving in a direction opposite to that of the first one, we have taken its velocity as negative.

total linear momentum before = m₁v₁ + m₂v₂

= 135,000x0.305 + 100,000x(−0.210)

= 135,000x0.305 - 100,000x0.210

= 20,175 kgm/s

Now we have to find total linear momentum after bumping. After the bumping both the train cars will be moving together with a common velocity(say v).

Therefore, total linear momentum after = mv

m = m₁ + m₂ = 135,000 + 100,000 = 235,000

total linear momentum before = total linear momentum after

235,000v = 20,175

v =
`(20,175)/(235,000)`

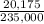
= 0.08585m/s