Answer: A. 664
Explanation:
Given : A marketing firm is asked to estimate the percent of existing customers who would purchase a "digital upgrade" to their basic cable TV service.
But there is no information regarding the population proportion is mentioned.
Formula to find the samples size , if the prior estimate to the population proportion is unknown :
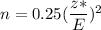
, where E = Margin of error.
z* = Two -tailed critical z-value
We know that critical value for 99% confidence interval =
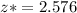 [By z-table]
[By z-table]
Margin of error = 0.05
Then, the minimum sample size would become :
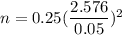
Simplify,
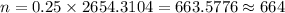
Thus, the required sample size= 664
Hence, the correct answer is A. 664.