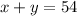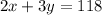Answer:
The system of equations for the given situation is:
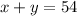
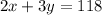
Explanation:
Given:
Regular basket is worth = 2 points
Long distance basket is worth =3 points
Total baskets in a game = 54
Total points in total = 118
 represents the number of regular baskets
represents the number of regular baskets
 represents the number of long distance baskets.
represents the number of long distance baskets.
Expression for total baskets can be given by ⇒
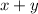
Thus first equation representing total baskets in a game is given by:
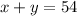
Since a regular basket is worth 2 points
So
 regular baskets would be worth
regular baskets would be worth
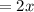 points
points
Since a long distance basket is worth 3 points
So
 long distance baskets would be worth
long distance baskets would be worth
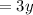 points
points
Expression for total points in a game can be given by ⇒
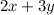
Thus second equation representing total points in a game is given by:
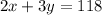
∴ The system of equations for the given situation is: