Question

The manufacturer of the ColorSmart-5000 television set claims 95 percent of its sets last at least five years without needing a single repair. In order to test this claim, a consumer group randomly selects 390 consumers who have owned a ColorSmart-5000 television set for five years. Of these 390 consumers, 303 say their ColorSmart-5000 television sets did not need a repair, whereas 87 say their ColorSmart-5000 television sets did need at least one repair. (a) Find a 99 percent confidence interval for the proportion of all ColorSmart-5000 television sets that have lasted at least five years without needing a single repair. (Round your answers to 3 decimal places.)

Answer 1

Explanation:

Hello!

Your study variable is X: "number of ColorSmart-5000 that didn't need repairs after 5 years of use, in a sample of 390"

X~Bi (n;ρ)

ρ: population proportion of ColorSmart-5000 that didn't need repairs after 5 years of use. ρ = 0.95

n= 390

x= 303

sample proportion ^ρ: x/n = 303/390 = 0.776 ≅ 0.78

Applying the Central Limit Theorem you approximate the distribution of the sample proportion to normal to obtain the statistic to use.

You are asked to estimate the population proportion of televisions that didn't require repairs with a confidence interval, the formula is:

^ρ±
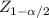`Z_(1-\alpha /2)`* √[(^ρ(1-^ρ))/n]

`Z_(1-\alpha /2)` =
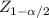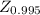`Z_(0.995)` = 2.58

0.78±2.58* √[(0.78(1-0.78))/390]

0.0541

[0.726;0.834]

With a confidence level of 99% you'd expect that the interval [0.726;0.834] contains the true value of the proportion of ColorSmart-5000 that didn't need repairs after 5 years of use.

I hope it helps!