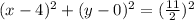Question

Write the equation in standard form for the circle with center (4,0) passing through 4,(11/2).

Answer 1

The standard equation of circle is
`(x-4)^2 + (y)^2  = ((11)/(2)) ^2`

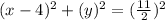
Explanation:

The given circle has Center = (4,0)

Passing through (4,11/2)

The standard form of the Circle is given as:

`(x-h)^2 + (y-k)^2  = r^2`

Here, (h,k) is the center coordinates and r : radius of the given circle.

So, here according to the question:

(h,k) = (4,0) , (x,y) = (4,11/2)

Putting the above value sin the equation of circle, determine the value of r:

`(4-4)^2 + ((11)/(2) -0)^2  = r^2\\\implies ((11)/(2)) ^2 = r^2\\\implies r = ((11)/(2))`

Hence, the standard equation of circle is
`(x-4)^2 + (y-0)^2  = ((11)/(2)) ^2`