Question

A collection of coins consists of nickels, dimes, and quarters. There are three fewer quarters than nickels and six more dimes than quarters. How many of each kind of coin is in the collection if the total value of the collection is $4.35?

PLEASE HELP ME THIS IS DUE TOMORROW!!!

Answer 1

You have 15 dimes. You have 9 quarters. You have 12 nickels

Explanation:

lets set some variables:

let "n" = the number of nickels

let "d" = the number of dimes

let "q" = the number of quarters

So, the total amount of money you have should be: $4.35 = 0.25q + 0.10d + 0.05n

Now let's look at the relationships between the coins:

"There are three fewer quarters than nickels": n - 3 = q

"six more dimes than quarters": q + 6 = d

So now you have three equations with three variables, all you need to do is solve.

`\left \{ {{4.35 = 0.25q + 0.10d + 0.05n} \atop {n - 3 = q}} \atop {q + 6 = d}}\right.`

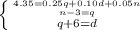
first, you can substitute "n-3" for "q" (according to the 2nd equation) in the 1st and 3rd equation, you get:

`\left \{ {{4.35=0.25(n-3)+0.10d+0.05n} \atop {(n-3)+6=d}} \right.`

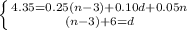
You now only have two equations and two variables.

Simplify:

`\left \{ {{4.35=0.25n-0.75+0.10d+0.05n} \atop {n+3=d}} \right.`

`\left \{ {{4.35=0.30n-0.75+0.10d} \atop {n+3=d}} \right.`

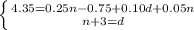
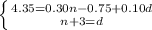
Now substitute "n+3" for "d" (according to the 2nd equation) in the 1st equation:

4.35=0.30n-0.75+0.10(n+3)

simplify:

4.35=0.30n-0.75+0.10n+0.30

4.35=0.40n-0.45

4.35+0.45=0.40n

4.80=0.40n

n=12

You have 12 nickels. Now sub "n" back into your equations to find the number of dimes and quarters:

n - 3 = q

12 - 3 = q

q = 9

You have 9 quarters.

q + 6 = d

9 + 6 = d

d = 15

You have 15 dimes.