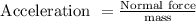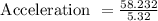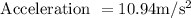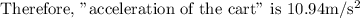Question

A shopper pushes a 5.32 kg grocery cart

with a 12.7 N force directed at -28.7°. A friction
force of 8.33 N pushes back against the motion.
What is the acceleration of the cart?​

Answer 1

Answer: 0.53

Explanation: Try looking it up on yahoo.

Answer 2

`\text { acceleration of the cart is } 10.94 \mathrm{m} / \mathrm{s}^(2)`

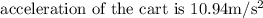
Step-by-step explanation:

According to “Newton's second law”

“Force” is “mass” times “acceleration”, or F = m× a. This means an object with a larger mass needs a stronger force to be moved along at the same acceleration as an object with a small mass

Force = mass × acceleration

`\text { Acceleration }=\frac{\text { force }}{\text { mass }}`

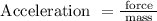
Given that,

Mass = 5.32 kg

`\text { Force }=12.7 \mathrm{N} \text { forces at }-28.7^(\circ)`

`x=-28.7^(\circ)`

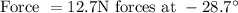
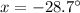
F = 12.7N

Normal force = mg + F sinx,

“m” being the object's "mass",

“g” being the "acceleration of gravity",

“x” being the "angle of the cart"

`\mathrm{g}=9.8 \mathrm{m} / \mathrm{s}^(2)\text { (g is referred to as the acceleration of gravity. Its value is } 9.8 \mathrm{m} / \mathrm{s}^ 2 \text { on Earth })`

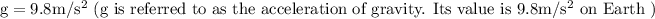
To find normal force substitute the values in the formula,

Normal force = 5.32 × 9.8 + 12.7 × sin(-28.7)

Normal force = 52.136 + 12.7 × 0.480

Normal force = 52.136 + 6.096

Normal force = 58.232 N

Acceleration of the cart:

`\text { Acceleration }=\frac{\text {Normal force}}{\text { mass }}`

`\text { Acceleration }=(58.232)/(5.32)`

`\text { Acceleration }=10.94 \mathrm{m} / \mathrm{s}^(2)`

`\text { Therefore,`