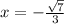Question

Suppose that f(x)=14x−6x3. (A) Find the average of the x values of all local maxima of f. Note: If there are no local maxima, enter -1000.

Answer 1

Maximum at
`x =(√(7))/(3)`

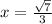
Explanation:

Given function,

`f(x) = 14x - 6x^3`

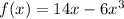
Differentiating with respect to x,

`f'(x) = 14 - 18x^2----(1)`

For critical values :

`f'(x) = 0`

`14 - 18x^2 =0`

`14 = 18x^2`

`x^2 = (14)/(18)`

`x^2=(7)/(9)`

`x = \pm (√(7))/(3)`

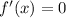
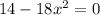
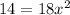
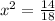
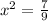
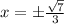
Now, differentiating equation (1) again with respect to x,

`f''(x) = -36x`

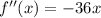
Since,

`f''((√(7))/(3)) = -36((√(7))/(3)) < 0`

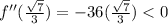
This means that the function is maximum at
`x=(√(7))/(3)`

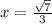
While,

`f''(-(√(7))/(3)) = 36((√(7))/(3)) > 0`

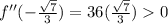
This means that the function is minimum at
`x=-(√(7))/(3)`