Question

What is the moment of inertia of an object that rolls without slipping down a 3.5-m- high incline starting from rest, and has a final velocity of 7.3 m/s? Express the moment of inertia as a multiple of MR2, where M is the mass of the object and R is its radius. (Hint: Use total conservation of mechanical energy)

Answer 1

I = 0.287 MR²

Step-by-step explanation:

given,

height of the object = 3.5 m

initial velocity = 0 m/s

final velocity = 7.3 m/s

moment of inertia = ?

Using total conservation of mechanical energy

change in potential energy will be equal to change in KE (rotational) and KE(transnational)

PE = KE(transnational) + KE (rotational)

`mgh = (1)/(2)mv^2 + (1)/(2)I\omega^2`

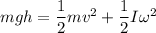
v = r ω

`mgh = (1)/(2)mv^2 + (1)/(2)(Iv^2)/(r^2)`

`I = (m(2gh - v^2)r^2)/(v^2)`

`I = (mr^2(2* 9.8 * 3.5 - 7.3^2))/(7.3^2)`

`I =mr^2(0.287)`

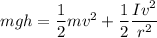
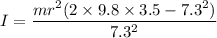
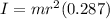
I = 0.287 MR²