Answer:
a)

b)
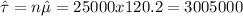
c)
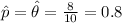
d) Median =120
Explanation:
1) Some important concepts
The mean refers to the "average that is used to derive the central tendency of data analyzed. It is determined by adding all the data points in a population and then dividing the total by the number of points".
Method of moments "involves equating sample moments with theoretical moments". For example the first sample moment about the origin is defined as
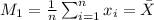
The median is "the middle number in a sorted, ascending or descending, list of numbers and can be more descriptive of that data set than the average".
When we are trying to estimate the population proportion, p.
All estimation is based on the fact that the normal can be used to approximate the binomial distribution when np and nq are both at least 5. Where p is the probability of success and q the probability of failure.
2) Part a
Using the method of the moments a point of estimate for the
 is:
is:

3) Part b
If
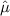 is an individual estimate for the average gas usage during January and
is an individual estimate for the average gas usage during January and
 represent "the total amount of gas used by all of these houses during January" then the estimation for the total would be given by:
represent "the total amount of gas used by all of these houses during January" then the estimation for the total would be given by:
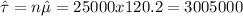
3) Part c
For this part we want to estimate p ="the proportion of all houses that used at least 100 therms". If X is the random variable who represent the number of houses that exceed the usage of 100, we see that 8 out of 10 values are above 100, so the random variable X would be distributed binomial
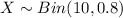 where n=10 and
where n=10 and
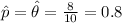
4) Part d
In order to find the median we need to put the data in order first, like this:
86,99,103,109,118,122,125,138,149,153
Since we have 10 observations and this number is even the procedure that we need to use in order to find the median is:
a) Find the value at position[n/2]=[10/2]=[5] on the data set ordered. For this case the value at position [5] is 118
b) Find the value at position[n/2 +1]=[10/2 +1]=[6] on the data set ordered. For this case the value at position [6] is 122
c) Find the average from the values obtained on steps a) and b). for this case (118+122)/2=120
So the Median = 120