Question

The U.S. Bureau of Labor Statistics reports that 11.3% of U.S. workers belong to unions. Suppose a sample of 400 U.S. workers is collected in 2014 to determine whether union efforts to organize have increased union membership at 0.025 level of significance. The sample results in a test statistic (z) of 2.2.

We conclude that union membership increased in 2014. (Enter 1 if the conclusion is correct. Enter 0 otherwise.)

Answer 1

1. The conclusion is statistically correct at the significance level given.

Explanation:

1) Data given and notation n

n=400 represent the random sample taken

X represent the people with union membership in the sample

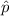`\hat p` estimated proportion of people with union membership in the sample

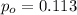`p_o=0.113` is the value that we want to test

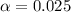`\alpha=0.025` represent the significance level (no given)

z would represent the statistic (variable of interest)

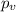`p_v` represent the p value (variable of interest)

p= population proportion of people with union membership

2) Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that the proportion of people with union membership exceeds 11.3%. :

Null Hypothesis:
`p \leq 0.113`

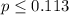
Alternative Hypothesis:
`p >0.113`

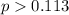
We assume that the proportion follows a normal distribution.

This is a one tail upper test for the proportion of union membership.

The One-Sample Proportion Test is "used to assess whether a population proportion
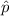`\hat p` is significantly (different,higher or less) from a hypothesized value
`p_o`".

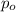Check for the assumptions that he sample must satisfy in order to apply the test

a)The random sample needs to be representative: On this case the problem no mention about it but we can assume it.

b) The sample needs to be large enough

`np_o =400*0.113=45.2>10`

`n(1-p_o)=400*(1-0.113)=354.8>10`

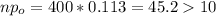
3) Calculate the statistic

The statistic is calculated with the following formula:

`z=\frac{\hat p -p_o}{\sqrt{(p_o(1-p_o))/(n)}}`

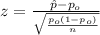
On this case the value of
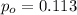`p_o=0.113` is the value that we are testing and n = 400.

Since we have already the statistic calculated z=2.2, we just need to calculate the p value in order to check if we can reject or not the null hypothesis.

4) Statistical decision

It's important to refresh the p value method or p value approach . "This method is about determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.

Based on the alternative hypothesis the p value would be given by:

`p_v =P(z>2.2)=1-P(z<2.2)=0.014`

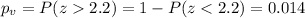
Using the significance level given
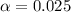`\alpha=0.025` we see that
`p_v<\alpha` so we have enough evidence at this significance level to reject the null hypothesis. And on this case makes sense the claim that the union membership increased in 2014.