Since the polynomial has roots of multiplicity 2 at x=5 and x=0, factors of (x−5) and( x=0 ) factors of
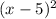 must be present. Also, since it has a root of multiplicity 1 at x=−1, the factor (x+1) must be present.
must be present. Also, since it has a root of multiplicity 1 at x=−1, the factor (x+1) must be present.
Since P(x) has a root of multiplicity 2 at x = 5, the factor
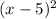 must be present in the polynomial. Similarly, since P(x) has a root of multiplicity 2 at x = 0, the factor
must be present in the polynomial. Similarly, since P(x) has a root of multiplicity 2 at x = 0, the factor
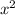 must be present. Additionally, since P(x) has a root of multiplicity 1 at x = -1, the factor (x + 1) must be present.
must be present. Additionally, since P(x) has a root of multiplicity 1 at x = -1, the factor (x + 1) must be present.
Therefore, a possible formula for P(x) is:
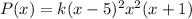
where k is a constant. Since the leading coefficient of P(x) is 1, we can solve for k by substituting x = 0 and setting P(x) = 1:
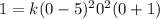
Solving for k, we find k = 1.
Therefore, a possible formula for P(x) is:
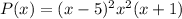
Complete question below:
The polynomial of degree 5, P(x), has leading coefficient 1, has roots of multiplicity 2 at x = 5 and x = 0, and a root of multiplicity 1 at x = -1. Find a possible formula for P(x).