To solve this problem it is necessary to use the conservation equations of both kinetic, rotational and potential energy.
By definition we know that

Where,
KE =Kinetic Energy
KR = Rotational Kinetic Energy
PE = Potential Energy
In this way
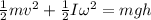
Where,
m = mass
v= Velocity
I = Moment of Inertia
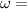 Angular velocity
Angular velocity
g = Gravity
h = Height
We know as well that
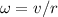 for velocity (v) and Radius (r)
for velocity (v) and Radius (r)
Therefore replacing we have
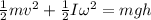
![[tex]h= (1)/(2) (v^2)/(g) +(1)/(2) (I)/(mg)((v)/(r))^2](https://img.qammunity.org/2020/formulas/physics/college/va3m09pz09g5zen7w7kyeix2q5agxtragk.png) [/tex]
[/tex]
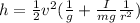
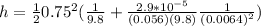
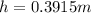
Therefore the height must be 0.3915 for the yo-yo fall has a linear speed of 0.75m/s