Question

A 2 kg ball with an initial velocity of 10 m/s moves at an angle 60º above the +x-direction. The ball hits a vertical wall and bounces off so that it is moving 60º above the −x-direction with the same speed.

What is the impulse delivered by the wall?

Answer 1

I = 20 i ^ N s

Step-by-step explanation:

For this problem let's use the Impulse equation

I = Δp = m
`v_(f)`- v₀

The impulse and the velocity are vector quantities, let's calculate on each axis, let's decompose the velocity

cos 60 = vₓ / v

vₓ = v cos 60

sin60 =
`v_(y)` / v

`v_(y)` = v sin60

vₓ = 10 cos 60

`v_(y)` = 10 sin60

vₓ = 5.0 m / s

`v_(y)` = 8.66 m / s

Let's calculate the impulse on each axis

X axis

Iₓ = m
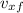`v_(xf)` - m vₓ₀

How the ball bounces

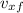`v_(xf)` = - vₓ₀ = vₓ

Iₓ = 2 m vₓ

Iₓ = 2 2 5

Iₓ = 20 N s

Y axis

`I_(y)` = m
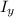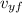`v_(yf)` - m vyo

On the axis and the ball does not change direction so

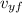`v_(yf)` = vyo

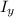`I_(y)` = 0

The total momentum is

I = Iₓ i ^ +
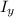`I_(y)` j ^

I = 20 i ^ N s