Question

Find the magnitude of the vector a and the smallest positive angle θ from the positive x-axis to the vector OP that corresponds to a. a=0,-5.

Answer 1

|a| = 5

θ = 90°

Explanation:

The position vector of a is OP.

`\vec{a}=<0,-5>`

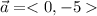
The magnitude of a vector is square root of of sum of square of x and y component.

x-component of vector a = 0

y-component of vector b = -5

`|a|=√(0^2+(-5)^2)`

`|a|=√(25)`

`|a|=5`

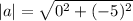
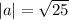
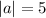
The smallest positive angle θ from the positive x-axis to the vector OP

`\theta = \tan^(-1)\frac{\text{y-component}}{\text{x-component}}`

`\theta=\tan^(-1)((-5)/(0))`

`\theta=\tan^(-1)(-\infty)`

`\theta=270^\circ\text{ and }-90^\circ`

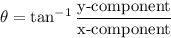
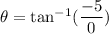
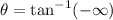
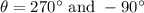
Smallest possible angle is 90° with positive direction of x-axis.

Hence, the magnitude of vector a is 5 and smallest possible angle is 90°