Question

Using Cramer's Rule, what is the value of x in the solution to the system of linear equations below?

5x-4 = 3y
2x+32 = 4y
ale
WIN
Ô CO

Answer 1

The value of X in the solution to the system of linear equations below

5x-4=3y

2x+32= 4y is 8.

Explanation:

Solution:

First write the expression in the form of ax by = c

Therefore the equations are as

`5x-3y=4\ and\\2x-4y=-32`

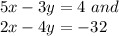
Now we will write in linear equation in matrix form

`\left[\begin{array}{cc}5&-3\\2&-4\end{array}{}\right] \left[\begin{array}{c}x\\y\end{array}{}\right]= \left[\begin{array}{c}4\\-32\end{array}{}\right]`

By Cramer's rule we have

`x = (Dx)/(D)`

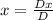
Where D is the determinant of 2 x 2 matrix

and Dx is the determinant after replacing the x coefficient by the constants

`Det\left[\begin{array}{cc}5&-3\\2&-4\end{array}{}\right]= 5*-4-(-3*2)\\\\=-20+6\\\therefore D= -14\\`

For Dx we will have

`Dx= \left[\begin{array}{cc}4&-3\\-32&-4\end{array}{}\right]= 4*-4-(-3* -32)\\\\=-16-96\\= -112\\\therefore Dx = -112`

Now by Cramer's rule

`x = (Dx)/(D)\\= (-112)/(-14)\\= 8\\ \therefore x = 8`