Question

2-phosphoglycerate(2PG) is converted to phosphoenolpyruvate (PEP) by the enzyme enolase. The standard free energy change(deltaGo’) for this reaction is +1.7 kJ/mol. If the cellular concentrations are 2PG = 0.5 mM and PEP = 0.1 mM, what is the free energy change at 37 oC for the reaction 2PG ↔ PEP?(A) 5.8 kJ/mol(B) -5.8 kJ/mol(C) +2.4 kJ/mol(D) -2.4 kJ/mol(E) -4146.4 kJ/mol(F) +4146.4 kJ/mol

Answer 1

The correct option is: (D) -2.4 kJ/mol

Step-by-step explanation:

Chemical reaction involved: 2PG ↔ PEP

Given: The standard Gibb's free energy change: ΔG° = +1.7 kJ/mol

Temperature: T = 37° C = 37 + 273.15 = 310.15 K (∵ 0°C = 273.15K)

Gas constant: R = 8.314 J/(K·mol) = 8.314 × 10⁻³ kJ/(K·mol) (∵ 1 kJ = 1000 J)

Reactant concentration: 2PG = 0.5 mM

Product concentration: PEP = 0.1 mM

Reaction quotient:
`Q_(r) =(\left [ PEP \right ])/(\left [ 2PG \right ]) = (0.1 mM)/(0.5 mM) = 0.2`

To find out the Gibb's free energy change at 37° C (310.15 K), we use the equation:

`\Delta G = \Delta G^(\circ ) + 2.303 R T log Q_(r)`

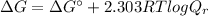
`\Delta G = 1.7 kJ/mol + [2.303 * (8.314 * 10^(-3) kJ/(K.mol))* (310.15 K)] log (0.2)`

`\Delta G = 1.7 + [5.938] * (-0.699) = 1.7 - 4.15 = (-2.45 kJ/mol)`

Therefore, the Gibb's free energy change at 37° C (310.15 K): ΔG = (-2.45 kJ/mol)