Question

If 6.50 moles of an ideal gas has a pressure of 2.69 atm, and a volume of 64.27 L, what is the temperature of the sample in degrees Celsius?

Answer 1

Answer: The temperature in degrees Celsius is 51.21ºC.

Step-by-step explanation:

An ideal gas is a hypothetical gas whose pressure-volume-temperature

behavior can be completely accounted for by the ideal gas equation:

`p×V = n×R×T`

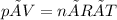
We want to know the temperature of the sample, which will be in Kelvin, so we rearrange the equation to give:

`T= p×V ÷ n×R`

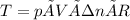
Knowing that:

p= 2.69 atm

n= 6.50 mol

V= 64. 27 L

and R, the gas constant is 0.082 L× atm ÷ mol×K

`T = 2.69 atm×64.27 L ÷ 6.50 mol×0.082 L.atm÷mol.K = <strong>324.36 K</strong>`

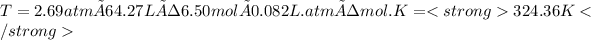
Now, we need to convert Kelvins to degrees Celsius. We use the following equation:

`K = (ºC + 273.15 ºC) × 1K ÷ 1ºC`

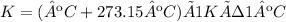
K= 324.36 K - 273.15ºC = 51.21 ºC

Therefore, the temperature of the sample is 51.21 degrees Celsius.