Question

A large bakery buys flour in 1500-pound bags. The bakery uses an average of 1,215 bags a year. Preparing an order and receiving a shipment of flour involves a cost of $10 per order. Annual carrying costs are $75 per bag. What order size would minimize the total cost?

Answer 1

18 units

Step-by-step explanation:

The computation of the economic order quantity is shown below:

=
`\sqrt{\frac{2* \text{Annual demand}* \text{Ordering cost}}{\text{Carrying cost}}}`

=
`\sqrt{\frac{2* \text{1,215}* \text{\$10}}{\text{\$75}}}`

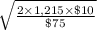
= 18 units

At 18 units of order size, the total cost would minimize.

It is that level at which the total carrying cost and the total ordering cost is equal.

Total cost = Purchase cost + ordering cost + carrying cost

It is a combination of purchase cost, ordering cost and the carrying cost